Horseshoe Falls
Participants
Gregory B. Pasternack, Bett. L. Valle, Christopher R. Ellis, Kyle A. Leier, Jeffrey D. Marr
Background
Hydraulic jumps are turbulent mixtures of air and water that produce significant energy dissipation, air entrainment, surface waves, and spray. Steep channel units such as cascades and steps may have >50% of stream area in a supercritical or jump condition. Despite the prevalence of natural hydraulic jumps in mountain streams, their role in flow mechanics, sediment transport, channel change, stream ecology, and basin evolution is largely unknown. What is known about them comes from studies using prismatic flumes and low bed resistance- both rare in mountain channels. Geomorphic studies of jumps rely on qualitative observations and use of crude equations whose assumptions are violated. Understanding mountain stream geomorphology and ecology, developing river restoration design tools, and modeling landscape evolution require investigation of actual channel processes, including those associated with hydraulic jumps.
The overall goal of the Pasternack Lab research program on waterfalls and hydraulic jumps is to investigate their mechanics and its relevance to fluvial geomorphology with the aid of new technologies that enable precise in situ field measurement for the first time.
River Truss Technology Enhancement With Fluid Mechanics Sensors
During late August 2003, the NSF-sponsored Second-generation River Truss (NSF Award EAR-0207713) and associated equipment was transported to the Saint Anthony Falls Laboratory (SAFL) in Minnesota for sensor development and trial application in a controlled laboratory setting. The specific objectives were to (1) exchange ideas with the instrumentation specialists at SAFL about possible sensors that could be used on the River Truss, (2) purchase, calibrate, and adapt the sensors to the River Truss, and (3) test the whole system in a study of the hydraulic jumps associated with common horseshoe waterfalls using SAFL's Main Test Channel.
The River Truss has an integrated vertical measuring rod (VMR) designed for surveying subaqueous bed topography and water surface topography in conjunction with a total station. The VMR is also designed to hold sensors for in situ measurement of fluid mechanics. Valle and Pasternack (2002) previously adapted low-cost time domain reflectometry sensors for use in measuring the air:water ratio in hydraulic jumps at <25 Hz. At SAFL, a Validyne DP15 differential pressure transducer was adapted for use on the truss and calibrated to measure high frequency pressure fluctuations in the flow or on the riverbed. Also, an AMTI UDW3 underwater 6D force and moment sensor was adapted for use on the VMR. This sensor can measure drag and lift forces, while accounting for the "cross-talk" interference caused by torques imposed by the flow on the test object placed into the flow at the desired location.
Analytical Model of Step Systematics
Before the new technologies could be used to run experiments in SAFL's Main Test Channel, it was necessary to develop an analytical model of step systematics capable of predicting hydraulic jump regime and energy dissipation for any combination of discharge put into the test channel and downstream tailwater level. Because previous work on hydraulic jumps emphasized minimizing erosion at the toe of dams and spillways, it neglected the key role of variable tailwater conditions common for natural bed steps. Thus, the new model provided a substantial generalization of the equations and facilitated the experimental design of the flume experiments.
The analytical model used in this study was the precursor to NSEAM 1.0. The main difference is that the model in this study assumed a static, uniform rectangular channel. In contrast, NSEAM 1.0 allows for nonuniform channel geometry through the step, which is important for natural mountain steps.
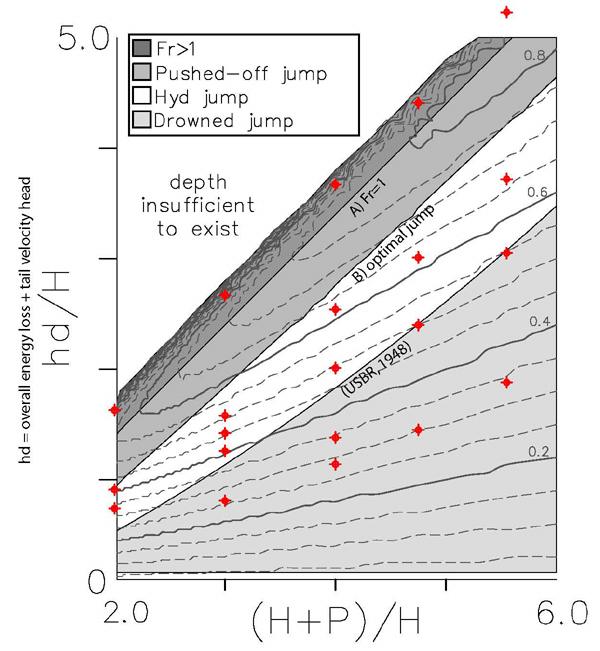
Figure below: Fractional energy dissipation (dashed grey lines) as a function of non-dimensional energy input (specific energy, H; step height, P) and degree of submergence (overall energy loss plus tail velocity head, hd). Hydraulic jump regimes for a rectangular free fall are shown as shaded regions. Conditions for the 21 experimental runs performed in this project are shown as red dots.
Horseshoe Falls Experiments
Methods
Horseshoe waterfalls are a common feature of steep bedrock rivers. As a first step toward understanding their geomorphology, a detailed study of the fluid mechanics at a 0.91-m vertical-drop, horseshoe waterfall was performed in a 2.75-m wide flume at SAFL (Fig. 3). Five non-dimensional upstream energy levels, each with 3-5 non-dimensional downstream tailwater depths (21 runs total), were assessed for water surface topography via digital elevation modeling, flow dynamics via digital videography, air content patterns using time domain reflectometry, lift and drag forces with a 6D force/moment sensor, and overall energy dissipation via an energy and momentum conservation model. Even though the primary goal was testing all of the equipment, it was possible to characterize the convergent hydraulics of a broad-crested horseshoe step with a plunging nappe. Details regarding the flume facility, experimental design, data acquision, and data analysis are published in Pasternack et al. (in press).
Below are two photos of the experimental broad-crested horseshoe step and data acquisition system over the falls during a drowned jump run.


Results
Regardless of tail depth, the horseshoe waterfall was found to have three distinct zones beyond the step brink- 1) a nappe whose degree of convergence depends on upstream energy and brink configuration, 2) a convergence zone whose features vary strongly with upstream energy, brink configuration, and tail depth, and 3) a downstream tailwater region whose dynamics primarily depend on tail depth (Fig. 4). The centerline nappe profile and brink velocity were reasonably predicted using RouseÕs jet trajectory equations when (H+P)/H>2. For any arbitrary broad-crested step brink configuration, maximum energy dissipation was found to occur when no jump was present and downstream tail depth was exactly critical. Rather than providing maximal energy dissipation, hydraulic jumps below steps provide efficient conversion of kinetic energy to potential energy.
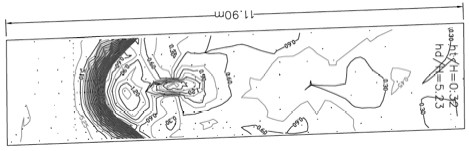
As an example, the figure below shows the non-dimensional (z/H) water surface topography for the horseshoe waterfalls under 1 of 21 mapped conditions, in this case low flow and low tailwater depth. Flow is left to right.
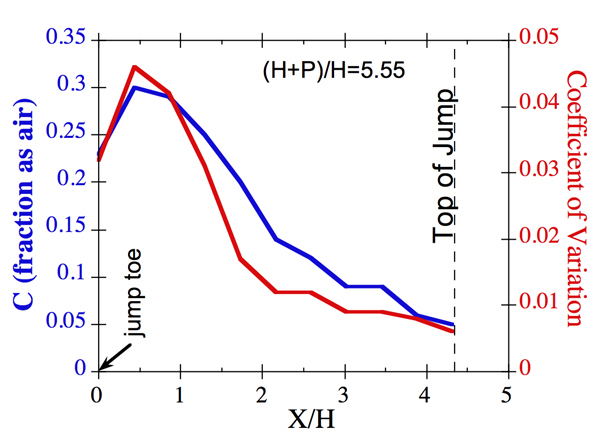
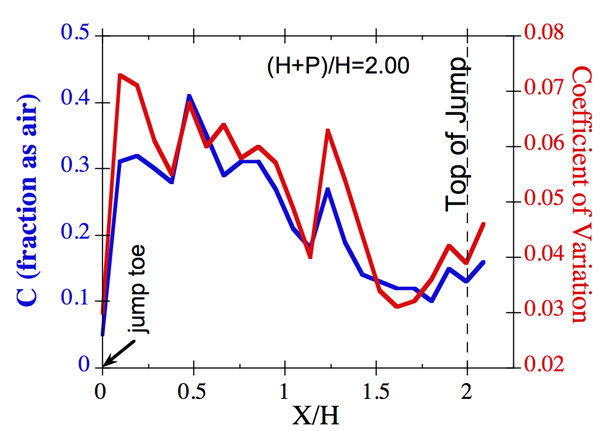
Longitudinal air content (C) profiles made from the step toe to the top of the hydraulic jump for each discharge at the tailwater level that just submerged the centerline of the jump toe showed some scale invariance (Fig. 5). The shape of the C profile and Cpeak in the hydraulic jump were scale invariant. Also, temporal fluctuations CÕ were scale invariant, showed the same profile as Cmean, and were typically 1-7% of Cmean. Videography of flow dynamics for the full range of discharge and tailwater conditions revealed a key scale dependence in the fluid mechanics resulting from the scale of aid-void implosions that were recorded. As ephemeral air pockets grew in size with increasing discharge, they suddenly exhibited a pattern of instability leading to massive implosions of the entire hydraulic jump at the highest discharge.
The two figures below show the air content profiles for the lowest ((H+P)/H=5.55)and B) highest ((H+P)/H=2.00) discharges.
The most remarkable results from the horseshoe waterfalls experiments at SAFL came from the measurements of lift and drag forces on the bed of the channel below the falls. Drag was smallest at the step toe and increased downstream to a peak on the downstream side of the boil beyond the hydraulic jump where flow accelerates again. Drag fluctuations scaled inversely and nonlinearly with the mean value, reaching an asymptote at ~10% of the mean value for high drag. For even small discharges, drag was sufficient to move bounders up to 2.8 m in diameter. In contrast, lift peaked under the hydraulic jump and its fluctuations were 1-10x of the mean value, suggesting that it too could move large boulders. These data suggest a mechanism in which lift force fluctuations dominate bed scour at the base of the falls. Then, material entrained off the bed are transported downstream by the drag force, which increased beyond the jump.
The two figures below show the profiles of drag and lift forces below a horseshoe falls for an experimental run.
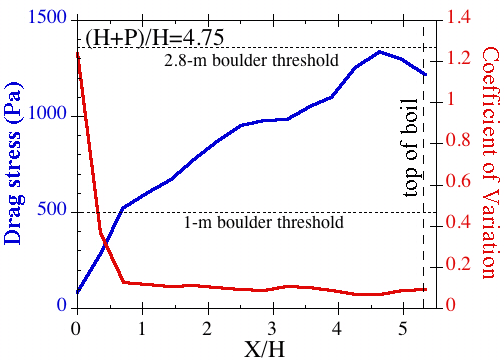
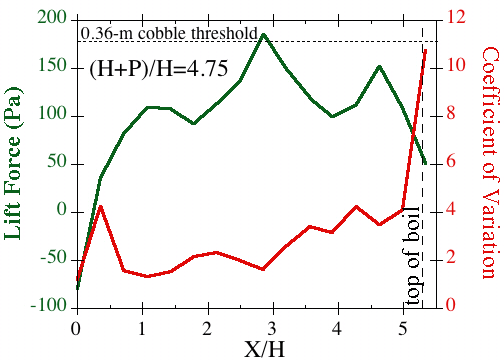
Conclusions
The primary outcome of this project was successful development of sensors for use with the River Truss to better understand the fluid mechanics and geomorphology of hydraulic jumps. In addition, a comprehensive study of horseshoe waterfalls was achieved that went beyond the original expectation of sensor testing. Pasternack et al. (2006) report on the analytical modeling and digital elevation analysis associated with the project.Specific conclusions included the following:
1. Regardless of tail depth, the horseshoe waterfall was found to have three distinct zones beyond the step brink- 1) a nappe whose degree of convergence depends on upstream energy and brink configuration, 2) a convergence zone whose features vary strongly with upstream energy, brink configuration, and tail depth, and 3) a downstream tailwater region whose dynamics primarily depend on tail depth.
2. The centerline nappe profile and brink velocity were reasonably predicted using Rouse's jet trajectory equations when (H+P)/H>2.
3. Peripheral profiles were not predictable using existing equations.
4. For any arbitrary broad-crested step brink configuration, maximum energy dissipation was found to occur when no jump was present and downstream tail depth was exactly critical. Rather than providing maximal energy dissipation, hydraulic jumps below steps provide efficient conversion of kinetic energy to potential energy.
Publications
- Pasternack, G.B., Ellis, C. Leier, K.A., Valle, B.L., Marr, J.D. 2006. Convergent hydraulics at horseshoe steps in bedrock rivers. Geomorphology 82:126-145.
- Pasternack, G. B., Ellis, C. R. and Marr, J. D. 2007. Jet and hydraulic jump near-bed stresses below a horseshoe waterfall, Water Resources Research 43, W07449, doi:10.1029/2006WR005774.
Acknowledgements
This material is based on work supported in part by the STC Program of the National Science Foundation under Agreement number EAR-0120914, in part by the Hydrology Program of the National Science Foundation under Agreement number EAR-0207713, and in part by private funding by the lead PI- Greg Pasternack. We thank Jon Hansberger, Sara Johnson, Omid Mohseni, Gary Parker, Mike Plante, Jared Roddy, Alfredo Santana, and Jeremy Schultz for assistance with experimental setup and data collection.


